锐角三角函数的性质
同步训练
1、假如∠A为锐角,且sinA=0.6,那样()
A.0°<A≤30° B.30°<A<45° C.45°<A<60° D.60°<A≤90°
2、已知sinα<cosplayα,那样锐角α的取值范围是()
A.30°<α<45° B.0°<α<45° C.45°<α<60° D.0°<α<90°
3、如图,A(0,8),B(0,2),点E为x轴正半轴上一动点,设tan∠AEB=m,则m的取值范围是()
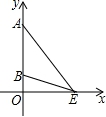
A.0<m≤ ![]() B.0<m≤
B.0<m≤![]() C.
C.![]() <m<
<m<![]() D.0<m≤
D.0<m≤![]()
4、如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度约为()(精准到0.1米,参考数据:
,则大楼AB的高度约为()(精准到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
A.30.6 B.32.1 C.37.9 D.39.4
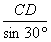
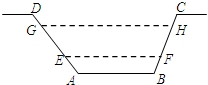
5、如图,某水渠的横断面是梯形,已知其斜坡AD的坡度为1:
1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是()米.
A.1.2 B.1.1 C.0.8 D.2.2
6、如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为18°,若楔子沿水平方向前移6cm(如箭头所示),则木桩上升了()
A.6tan18°cm B.![]() cm C.6sin18°cm D.6cosplay18°cm
cm C.6sin18°cm D.6cosplay18°cm
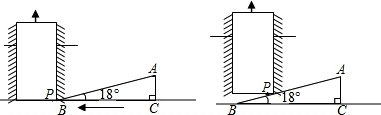
7、如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这个时候测得太阳光线与水平线的夹角为60°,则树BC的高度为 __________ 米.
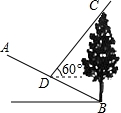
8、某货站用传送带传送货物,为了提升传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度i=1:![]() 的新传送带AC(如图所示).已知原传送带AB的长是4
的新传送带AC(如图所示).已知原传送带AB的长是4![]() 米.那样新传送带AC的长是__________米.
米.那样新传送带AC的长是__________米.
9、若α、β均为锐角,则以下有4个命题:
①若sinα<sinβ,则α<β;
②若α+β=90°,则sinα=cosplayβ;
③存在一个角α,使sinα=1.02;
④tanα=![]() .其中正确命题的序号是 __________.(多填或错填得0分,少填的酌情给分)
.其中正确命题的序号是 __________.(多填或错填得0分,少填的酌情给分)
10、(1)如图锐角的正弦值和余弦值都伴随锐角的确定而确定,变化而变化,试探索伴随锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)依据你探索到的规律试比较18°,34°,50°,62°,88°,这类锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“>”“=”“<”号),
若α=45°,则sinα__________cosplayα;
若0°<α<45°,则sinα __________cosplayα;
若45°<α<90°,sinα __________cosplayα.
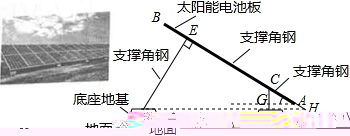
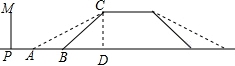
11、太阳能光伏发电因其清洗、安全、便利、高效等特征,已成为世界各国常见关注和重点进步的新兴产业.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号).
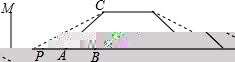
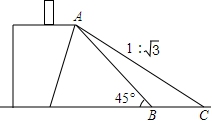
12、某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:
1,为了便捷行人推车过天桥,有关部门决定减少坡度,使新坡面的坡度为1:![]()
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是不是需要拆除?请说明理由

参考答案
1、分析:由sin30°=![]() =0.5,sin45°=
=0.5,sin45°=![]() ≈0.707,sinA=0.6,且sinα随α的增大而增大,即可求得答案.
≈0.707,sinA=0.6,且sinα随α的增大而增大,即可求得答案.
解:∵sin30°=![]() =0.5,sin45°=
=0.5,sin45°=![]() ≈0.707,sinA=0.6,且sinα随α的增大而增大,
≈0.707,sinA=0.6,且sinα随α的增大而增大,
∴30°<A<45°.
故选B
2、分析:第一依据正余弦的转换办法,得:cosplayα=sin(90°-α),又sinα<cosplayα,即sinα<sin(90°-α),再依据正弦值伴随角的增大而增大,进行剖析.
解:∵cosplayα=sin(90°-α),
∴sinα<cosplayα=sin(90°-α).
又正弦值伴随角的增大而增大,
得α<90°-α,
∴α<45°.
又α是锐角,则α的取值范围是0°<α<45度.
故选B.
3、分析:点E为x轴正半轴上一动点,设tan∠AEB=m,则m>0,再求出m的最大值即可.过A、B、E三点的圆O′与x轴相切时,∠AEB最大,m的值最大.作O′D⊥AB于D,由垂径定理得出AD=DB=![]() AB=3,OD=OA-AD=5,那样⊙O′的半径为5.在直角△O′AD中,由勾股定理得出O′D=
AB=3,OD=OA-AD=5,那样⊙O′的半径为5.在直角△O′AD中,由勾股定理得出O′D=![]() =4,则AE=
=4,则AE=![]() =4
=4![]() ,再作BC⊥AE于C.由S△AOE=
,再作BC⊥AE于C.由S△AOE= ![]() OA•OE=S△BOE+S△ABE,求出BC=
OA•OE=S△BOE+S△ABE,求出BC= ![]() ,CE=
,CE= ![]() =
=![]() ,那样m的最大值为
,那样m的最大值为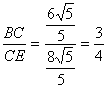 .
.
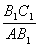
解:如图,过A、B、E三点的圆O′与x轴相切时,∠AEB最大.
作O′D⊥AB于D,则AD=DB=![]() AB=3,
AB=3,
∵OA=8,
∴OD=OA-AD=5,
∴O′E=O′A=OD=5,即⊙O′的半径为5.
在直角△O′AD中,由勾股定理得O′D= O′D=![]() =4,
=4,
∴OE=O′D=4,
∴AE= ![]() =4
=4![]() ,,
,,
作BC⊥AE于C.
∵S△AOE=![]() OA•OE=S△BOE+S△ABE,
OA•OE=S△BOE+S△ABE,
∴![]() ×8×4=
×8×4=![]() ×2×4+
×2×4+![]() ×4
×4![]() ×BC,
×BC,
∴BC=![]() ,
,
∵BE2=OB2+OE2=22+42=20,
∴CE=![]() =
=![]() ,,
,,
∴m的最大值为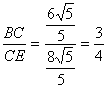 ,
,
又∵m>0,
∴0<m≤![]()
故选A
4、分析:延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH=![]() x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6
x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6![]() 米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6
米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6![]() +20(米),即可得出大楼AB的高度.
+20(米),即可得出大楼AB的高度.

解:延长AB交DC于H,作EG⊥AB于G,如图所示:
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:![]() ,
,
∴BH:CH=1:![]()
设BH=x米,则CH=![]() x米,
x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+(![]() x)2=122,
x)2=122,
解得:x=6,∴BH=6米,CH=6![]() 米,
米,
∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=6![]() +20(米),
+20(米),
∵∠α=45°,
∴∠EAG=90°-45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6![]() +20(米),
+20(米),
∴AB=AG+BG=6![]() +20+9≈39.4(米);
+20+9≈39.4(米);
故选:D
5、分析:过点E作EM⊥GH于点M,过点F作FN⊥GH于点N,可得四边形EFNM为矩形,可得MN=EF,然后设ME=FN=x,分别在Rt△GME和Rt△NHF中表示出GM和HN的长度,最后依据GH=6米,列出方程求出x的值.
解:过点E作EM⊥GH于点M,过点F作FN⊥GH于点N,
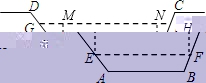
可得四边形EFNM为矩形,
则MN=EF,
设ME=FN=x,
在Rt△GME中,
∵斜坡AD的坡度为1:
1.2,
∴ME:GM=1:
1.2,
∴GM=1.2x,
在Rt△NHF中,
∵斜坡BC的坡度为1:0.8,
∴NF:NH=1:0.8,
∴NH=0.8x,
则GH=1.2x+0.8x+3.8=6,
解得:x=1.1.
故选B.
6、分析:依据已知,运用直角三角形和三角函数得到上升的高度.
解:由已知图形可得:tan18°=![]() ,
,
木桩上升的高度h=6tan18°cm.
故选:A.
7、分析:依据题意第一借助勾股定理得出DF,DE的长,再借助锐角三角函数关系得出EC的长,进而得出答案.
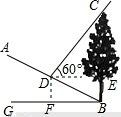
解:过点D作DF⊥BG,垂足为F,
∵斜坡AB的坡度i=1:2,
∴设DF=x,BF=2x,则DB=10m,
∴x2+(2x)2=102,
解得:x=2![]() ,
,
故DE=4![]() ,BE=DF=2
,BE=DF=2![]() ,
,
∵测得太阳光线与水平线的夹角为60°,
∴tan60°=![]() =
=![]() =
=![]() ,
,
解得:EC=4![]() ,
,
故BC=ED+BE=2![]() +4
+4![]() (m),
(m),
故答案为:2![]() +4
+4![]()
8、分析:依据题意第一得出AD,BD的长,再借助坡角的概念得出DC的长,再结合勾股定理得出答案.
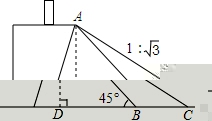
解:过点A作AD⊥CB延长线于点D,
∵∠ABD=45°,
∴AD=BD,
∵AB=4![]() ,
,
∴AD=BD=ABsin45°=4![]() ×
×![]() =4,
=4,
∵坡度i=1:![]() ,∴
,∴![]() =
=![]() =
=![]() ,则DC=4
,则DC=4![]() ,故AC=
,故AC=![]() =8(m).故答案为:8.
=8(m).故答案为:8.
9、分析:依据锐角三角函数正弦值随角度的增大而增大,与正弦余弦值与各边关系即可得出答案.
解:∵sinα<sinβ,则α<β;
故此选项正确;
②若α+β=90°,则sinα=cosplay(90°-α)=cosplayβ,
∴故此选项正确;
③存在一个角α,sinα=![]() ,
,
∴sinα≤1,
∴sinα=1.02,故此选项错误;
④tanα=![]() .依据对应边之间关系得出,
.依据对应边之间关系得出,
故此选项正确.
故答案为:①②④.
10、分析:(1)依据锐角三角函数的定义,即可发现伴随一个锐角的增大,它的对边在渐渐增大,它的邻边在渐渐减小,故正弦值伴随角的增大而增大,余弦值伴随角的增大而减小.
(2)依据上述规律,要比较锐角三角函数值的大小,仅需比较角的大小.
(3)依据定义与等腰三角形的性质,显然45°的正弦值和余弦值是相等的,再依据锐角三角函数值的变化规律,即可得到结论.
解:(1)在图中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=![]() ,sin∠B2AC=
,sin∠B2AC=![]() ,sin∠B3AC=
,sin∠B3AC=![]() ,
,
而![]() >
>![]() >
>![]() ,
,
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图中,Rt△ACB3中,∠C=90°,
cosplay∠B1AC=![]() ,cosplay∠B2AC=
,cosplay∠B2AC=![]() ,cosplay∠B3AC=
,cosplay∠B3AC=![]() ,
,
∵AB3>AB2>AB1,
∴![]() >
>![]() >
>![]() .
.
即cosplay∠B3AC<cosplay∠B2AC<cosplay∠B1AC;
结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
(2)由(1)可知:
sin88°>sin62°>sin50°>sin34°>sin18°;
cosplay88°<cosplay62°<cosplay50°<cosplay34°<cosplay18°.
(3)若α=45°,则sinα=cosplayα;若0°<α<45°,则sinα<cosplayα;若45°<α<90°,则sinα>cosplayα.
故答案为:=,<,>.
11、分析:过A作AG⊥CD于G,在Rt△ACG中,求得CG=25,连接FD并延长与BA的延长线交于H,在Rt△CDH中,依据三角函数的概念得到CH=90,在Rt△EFH中,依据三角函数的概念即可得到结论.
解:过A作AG⊥CD于G,则∠CAG=30°,
在Rt△ACG中,CG=ACsin30°=50×![]() =25,
=25,
∵GD=50-30=20,∴CD=CG+GD=25+20=45,
连接FD并延长与BA的延长线交于H,则∠H=30°,
在Rt△CDH中,CH=![]() =2CD=90,
=2CD=90,
∴EH=EC+CH=AB-BE-AC+CH=300-50-50+90=290,
在Rt△EFH中,EF=EH•tan30°=290×![]() =
=![]() ,
,
答:支撑角钢CD和EF的长度各是45cm,![]() cm
cm

12、分析:(1)由新坡面的坡度为1:![]() ,可得tanα=tan∠CAB=
,可得tanα=tan∠CAB= ![]() =
=![]() ,然后由特殊角的三角函数值,求得答案;
,然后由特殊角的三角函数值,求得答案;
(2)第一过点C作CD⊥AB于点D,由坡面BC的坡度为1:
1,新坡面的坡度为1:![]() .即可求得AD,BD的长,继而求得AB的长,则可求得答案.
.即可求得AD,BD的长,继而求得AB的长,则可求得答案.
解:(1)∵新坡面的坡度为1:![]() ,
,
∴tanα=tan∠CAB=![]() =
=![]() ,
,
∴∠α=30°.
答:新坡面的坡角a为30°;
(2)文化墙PM无需拆除.过点C作CD⊥AB于点D,则CD=6,
∵坡面BC的坡度为1:
1,新坡面的坡度为1:![]() ,∴BD=CD=6,AD=6
,∴BD=CD=6,AD=6![]() ,
,
∴AB=AD-BD=6![]() -6<8,∴文化墙PM无需拆除.
-6<8,∴文化墙PM无需拆除.